


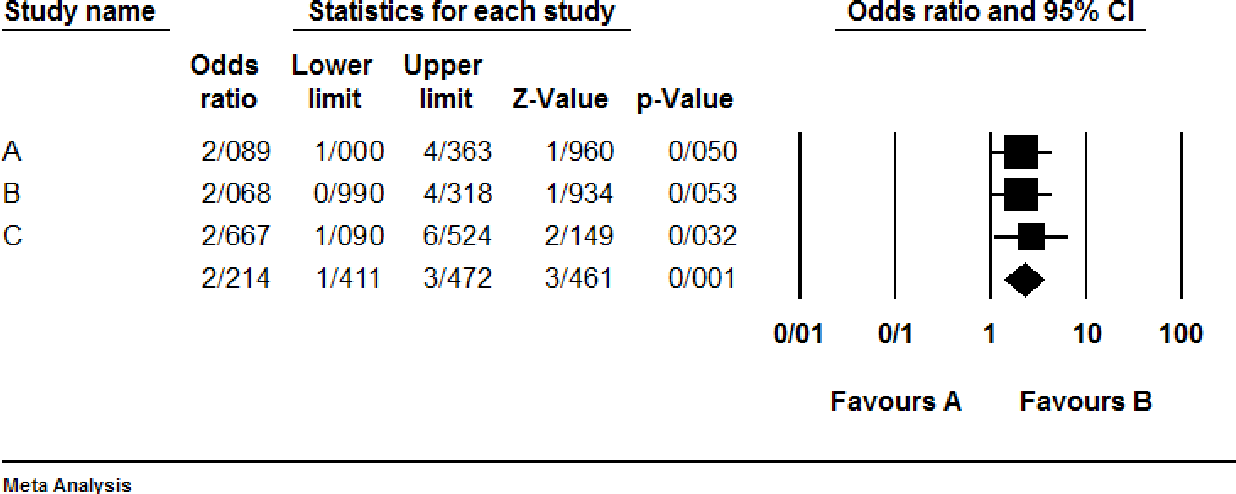
The figure below shows different measures. The different measures of these ratios allow drawing of statistical inferences of higher suitability or relevance. In simple terms, risk ratio is the ratio of two risks and odds ratio is the ratio of two odds. CMA also allows to calculate varied statistical versions of these classical effect measures, as shown in the figure below. When dealing with dichotomous outcomes, such as the number of events, ‘Risk ratio’, ‘Odds ratio’ or ‘Risk difference’ can be selected. These are not useful when the studies use non-natural units of scale, such as test scores because such scales do not have a natural zero point. Response ratios are useful when the outcome has been measured on a ratio scale. It is used when the outcome is measured on a physical scale such as length, weight, which it is unlikely to be zero. CMA does not offer the calculation of response ratio effect sizes. Note: The ‘log proportional change in the means of treatment and control group’ constitutes response ratio (Lajeunesse 2011). Standard deviation difference calculation uses following formula: Formula for standard deviation pooled for calculating effect size of single or matched groups The matched groups and one group (pre-post) designs also utilize standard deviation difference.
Formula for standard deviation pooled for calculating effect size for comparison groups The difference between the standard deviation of pre-post scores, within a single group is standard deviation difference. Whereas the pooled standard deviation of the treatment and control groups (independent or unmatched) is common standard deviation and is calculated using. In CMA certain formats demand standard deviation difference, while common standard deviation of difference is required by others. The important point of consideration arises with respect to the standard deviation, while comparing the results from different study designs having different study groups. This creates a standard index used to compare the outcomes across different studies. The standardized measures include dividing the mean difference in each study by the respective standard deviation. In such scenarios, resort to the measures of standardized mean difference (SMD). Whereas, if the studies report results or outcomes over different instruments, then raw difference can be used. If all the studies report results or outcomes over the same scale of measurement then difference in means can be directly calculated. The CMA software, allows to calculate difference in means (Raw mean difference, unstandardized), standard difference in means, Standard paired difference and Hedge’s g (Standardized mean differences), for continuous outcomes. Figure 2: Selecting effect size for continuous outcome Effect size for continuous outcomes The figure below shows the decision flow which could assist the in selecting the appropriate effect size for the study. The different types of outcomes constitute continuous (mean and standard deviation), binary data, and correlations. This will help the fulfillment of research goals and objectives. As a result, while conducting a meta-analysis, it is essential to select the appropriate effect size measure. Figure 1: Different types of effect size indices depending on the type of outcome Different outcomes of different effect sizeĭifferent study designs yield different outcomes, whether primary or secondary. The figure below shows the different effect size measures computable in CMA, as determined by the different types of outcomes.
They involve events or non-events or mean and standard deviation or other, where the measure of effect size also changes. This is important because different studies generate different datasets of variable nature. It will help to understand and choose appropriate effect size measure for analyzing data. The article will introduce the concept of different effect size measures. For any given study the effect size cannot be constrained to a single index or measure. It is the magnitude or size of an effect and usually refers to treatment effect in comprehensive meta analysis (CMA). The discussion surrounding meta analysis has effect size at the prime spot. Yashika Kapoor and Priya Chetty on October 31, 2017


 0 kommentar(er)
0 kommentar(er)
